2 一、總則
生物檢定法是利用生物體包括整體動物、離體組織、器官、細胞和微生物等評估藥物生物活性的一種方法。它以藥物的藥理作用爲基礎,以生物統計爲工具,運用特定的實驗設計在一定條件下比較供試品和相當的標準品或對照品所產生的特定反應,通過等反應劑量間比例的運算或限值劑量引起的生物反應程度,從而測定供試品的效價、生物活性或雜質引起的毒性。
生物檢定統計法主要敘述應用生物檢定時必須注意的基本原則、一般要求、實驗設計及統計方法。有關品種用生物檢定的具體實驗條件和要求,必須按照該品種生物檢定法項下的規定。
2.1 生物檢定標準品
凡中國藥典規定用生物檢定的品種都有它的生物檢定標準品(S)。S都有標示效價,以效價單位 (u)表示,其含義和相應的國際標準品的效價單位一致。
2.2 供試品
供試品(T)或(U)是供檢定其效價的樣品,它的活性組分應與標準品基本相同。
AT或AU是T或U的標示量或估計效價。
2.3 等反應劑量對比
生物檢定是將T和其S在相同的實驗條件下同時對生物體或其離體器官組織等的作用進行比較,通過對比,計算出它們的等反應劑量比值(R),以測得T的效價PT。
R是S和T等反應劑量(dS、dT)的比值,即R=dS/dT。M是S和T的對數等反應劑量(xS、sT)之差,即M=lgdS-lgdT=xS-xT 。 R=antilgM。
PT是通過檢定測得T的效價含量,稱T的測得效價,是將效價比值(R)用T的標示量或估計效價AT校正之後而得,即PT=AT·R或PT=AT·antilgM。
檢定時,S按標示效價計算劑量,T按標示量或估計效價(AT)計算劑量,注意調節T的劑量或調整其標示量或估計效價,使S和T的相應劑量組所致的反應程度相近。
2.4 生物變異的控制
生物檢定具有一定的實驗誤差,其主要來源是生物變異性。因此生物檢定必須注意控制生物變異,或減少生物變異本身,或用適宜的實驗設計來減小生物變異對實驗結果的影響,以減小實驗誤差。控制生物變異必須注意以下幾點。
(1)生物來源、飼養或培養條件必須均一。
(2)對影響實驗誤差的條件和因子,在實驗設計時應儘可能作爲因級限制,將選取的因級隨機分配至各組。例如體重、性別、窩別、雙碟和給藥次序等都是因子,不同體重是體重因子的級,雌性、雄性是性別因子的級,不同窩的動物是窩別因子的級,不同雙碟是碟間因子的級,給藥先後是次序因子的級等。按程度劃分的級(如動物體重),在選級時,應選動物較多的鄰近幾級,不要間隔跳越選級。
(3)按實驗設計類型的要求將限制的因級分組時,也必須嚴格遵守隨機的原則。
2.5 誤差項
指從實驗結果的總變異中分去不同劑量及不同因級對變異的影響後,剩餘的變異成分,用方差(S2)表示。對於因實驗設計類型的限制無法分離的變異成分,或估計某種因級對變異的影響小,可不予分離者,都併入S2。但劑間變異必須分離。
不同的檢定方法和實驗設計類型,分別按有關的公式計算S2。
2.6 可靠性測驗
平行線檢定要求在實驗所用的劑量範圍內,對數劑量的反應(或反應的函數)呈直線關係,供試品和標準品的直線應平行。可靠性測驗即驗證供試品和標準品的對數劑量反應關係是否顯著偏離平行偏離直線,對不是顯著偏離平行偏離直線(在一定的概率水平下)的實驗結果,認爲可靠性成立,方可按有關公式計算供試品的效價和可信限。
2.7 可信限和可信限率
可信限(FL)標誌檢定結果的精密度。M的可信限是M的標準誤SM和t值的乘積(t·SM),用95%的概率水平。M+t·SM是可信限的高限;M-t·SM是可信限的低限。用其反對數計算得R和PT的可信限低限及高限,是在95%的概率水平下從樣品的檢定結果估計其真實結果的所在範圍。
R或PT的可信限率(FL%)是用R或PT的可信限計算而得。效價的可信限率爲可信限的高限與低限之差除以2倍平均數(或效價)後的百分率。

計算可信限的t值是根據s2的自由度(f)查t值表而得。t值與f的關係見表一。
表一 t值表(P=0.95)
f | t |
3 4 5 6 7 8 9 10 11 12 | 3.18 2.78 2.57 2.45 2.37 2.31 2.26 2.23 2.20 2.18 |
f | t |
14 | 2.15 |
16 | 2.12 |
18 | 2.10 |
20 | 2.09 |
25 | 2.06 |
30 | 2.04 |
40 | 2.02 |
60 | 2.00 |
120 | 1.98 |
∞ | 1.96 |
各品種的檢定方法項下都有其可信限率的規定,如果檢定結果不符合規定,可縮小動物體重範圍或年齡範圍,或調整對供試品的估計效價或調節劑量,重複實驗以減小可信限率。
對同批供試品重複試驗所得n次實驗結果(包括FL%超過規定的結果),可按實驗結果的合併計算法算得PT的均值及其FL%作爲檢定結果。
3 二、直接測定法
直接測得藥物對各個動物最小效量或最小致死量的檢定方法。如洋地黃及其製劑的效價測定。
xS和xT爲S和T組各只動物的對數最小致死量,它們的均值xS和xT爲S和T的等反應劑量,nS和nT爲S和T組的動物數。
3.1 1.效價計算
按(1)~(3)式計算M、R和PT。
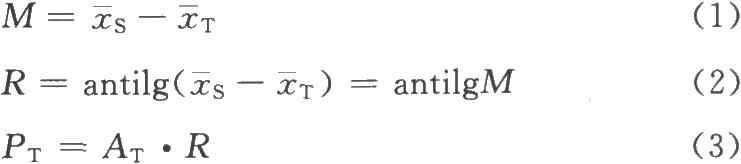
3.2 2.誤差項及可信限計算
按(4)~(8)式計算s2、SM及R或PT的FL和FL%。
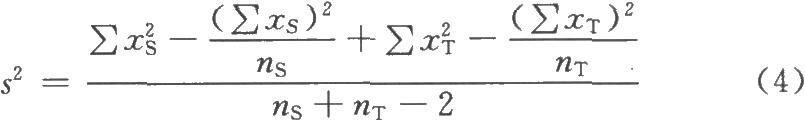
f=ns+nT-2,用此自由度查表一得t值。
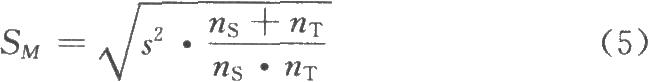

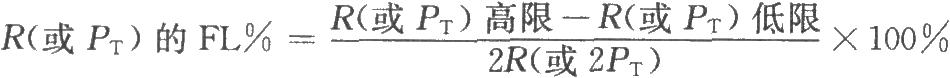 (8)
(8)
當兩批以上供試品(T、U…)和標準品同時比較時,按(9)式計算S、T、U的合併方差S2。
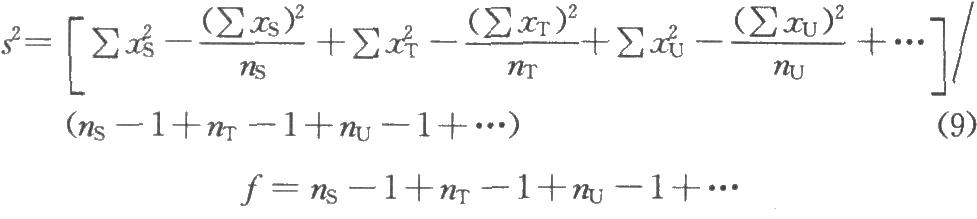
效價PT、PU…則是T、U分別與S比較,按(1)~(3)式計算。
例1 直接測定法
S爲洋地黃標準品,按標示效價配成1.0u/ml的酊劑,臨試驗前稀釋25倍。
T爲洋地黃葉粉,估計效價AT=10u/g,配成1.0u/ml的酊劑,臨試驗前配成稀釋液(1→25)。測定結果見表1-1。
S | T | ||
MLDs (dS) | xS | MLDT (dT) | xT |
u/kg體重 | lg(dS×10) | u/kg體重 | lg(dT×10) |
1.15 1.01 1.10 1.14 1.06 0.95 | 1.061 1.004 1.041 1.057 1.025 0.978 | 1.11 1.23 1.06 1.31 0.94 1.36 | 1.045 1.090 1.025 1.117 0.973 1.134 |
∑xs xS | 6.166 1.028 | ∑xT
| 6.384 1.064 |

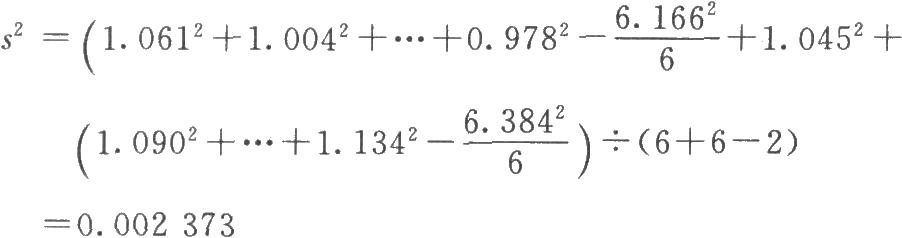

4 三、量反應平行線測定法
藥物對生物體所引起的反應隨着藥物劑量的增加產生的量變可以測量者,稱量反應。量反應檢定用平行線測定法,要求在一定劑量範圍內,S和T的對數劑量x和反應或反應的特定函數y呈直線關係,當S和T的活性組分基本相同時,兩直線平行。本版藥典量反應檢定主要用(2.2)法、(3.3)法或(2.2.2)法、(3.3.3)法,即S、T(或U)各用2個劑量組或3個劑量組,統稱(k·k)法或(k·k·k)法;如果S和T的劑量組數不相等,則稱(k·k')法;前面的k代表S的劑量組數,後面的k或k’代表T的劑量組數。一般都是按(k·k)法實驗設計,當S或T的端劑量所致的反應未達閾值,或趨於極限,去除此端劑量後,對數劑量和反應的直線關係成立,這就形成了(k·k')法。例如(3.3)法設計就可能形成(2.3)法或(3.2)法等。因此,(k·k')法中的k只可能比k'多一組或少一組劑量。(k·k')法的計算結果可供重複試驗時調節劑量或調整供試品估計效價時參考。無論是(k·k)法、(k·k')法或(k·k·k)法,都以K代表S和T的劑量組數之和,故K=k+k或K=k+k'或K=k+k+k。
本版藥典平行線測定法的計算都用簡算法,因此對各種(k·k)法要求:
(1)S和T相鄰高低劑量組的比值(r)要相等,一般r用(1:0.8)~(1:0.5),lgr=I。
4.1 1.平行線測定的實驗設計類型
根據不同的檢定方法可加以限制的因級數採用不同的實驗設計類型。本版藥典主要用下面三種實驗設計類型。
4.1.1 (1)隨機設計
劑量組內不加因級限制,有關因子的各級隨機分配到各劑量組。本設計類型的實驗結果只能分離不同劑量(劑間)所致變異,如絨促性素的生物檢定。
4.1.2 (2)隨機區組設計
將實驗動物或實驗對象分成區組,一個區組可以是一窩動物、一隻雙碟或一次實驗。在劑量組內的各行間加以區組間(如窩間、碟間、實驗次序間)的因級限制。隨機區組設計要求每一區組的容量(如每一窩動物的受試動物只數、每一隻雙碟能容納的小杯數等)必須和劑量組數相同,這樣可以使每一窩動物或每一隻雙碟都能接受到各個不同的劑量。因此隨機區組設計除了從總變異中分離劑間變異之外,還可以分離區組間變異,減小實驗誤差。例如抗生素杯碟法效價測定。
4.1.3 (3)交叉設計
同一動物可以分兩次進行實驗者適合用交叉設計。交叉設計是將動物分組,每組可以是一隻動物,也可以是幾隻動物,但各組的動物只數應相等。標準品(S)和供試品(T)對比時,一組動物在第一次試驗時接受S的一個劑量,第二次試驗時則接受T的一個劑量,如此調換交叉進行,可以在同一動物身上進行不同試品、不同劑量的比較,以去除動物聞差異對實驗誤差的影響,提高實驗精確度,節約實驗動物。(2.2)法S和T各兩組劑量,用雙交叉設計,將動物分成四組;對各組中的每一隻動物都標上識別號。每一隻動物都按給藥次序表進行兩次實驗。
雙交叉設計兩次實驗的給藥次序表
第一組 | 第二組 | 第三組 | 第四組 | |
第一次實驗 第二次實驗 | dS1 dT2 | dS2 dT1 | dT1 dS2 | dT2 dS1 |
4.2 2.平行線測定法的方差分析和可靠性測驗
(l)將反應值或其規定的函數(y)按S和T的劑量分組列成方陣表見表二。
表二 劑量分組方陣表

方陣中,K爲S和T的劑量組數和,m爲各劑量組內y的個數,如爲隨機區組設計,m爲行間或組內所加的因級限制;n爲反應的總個數,n=mK。
(2)特異反應剔除和缺項補足
特異反應剔除 在同一劑量組內的各個反應中,如出現個別特大或特小的反應,應按下法判斷其是否可以剔除。
設ya表示特異反應值(或其規定的函數),ym爲與ya相對的另一極端的反應值,y2、y3爲與ya最接近的兩個反應值,ym-1、ym-2爲與ym最接近的兩個反應值,m是該劑量組內的反應個數,將各數值按大小次序排列如下:
ya、y2、y3…ym-2、ym-1、ym
如ya爲特大值,則依次遞減,ym最小;如ya爲特小值,則依次遞升,ym最大。按(10)~(12)式計算J值。
當m=3~7時

當m=8~13時

當m=14~20時

如,的計算值大於J值表(表三)中規定的相應數值時,ya即可剔除。
表三 剔除特異反應的J值表
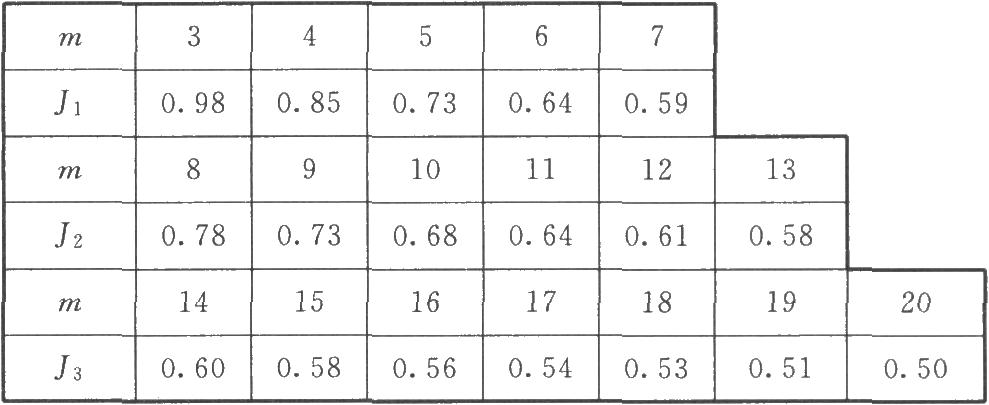
缺項補足 因反應值被剔除或因故反應值缺失造成缺項,致m不等時,根據實驗設計類型做缺項補足,使各劑量組的反應個數m相等。
隨機設計 對缺失數據的劑量組,以該組的反應均值補入,缺1個反應補1個均值,缺2個反應補2個均值。
隨機區組設計 按(13)式計算,補足缺項。

如果缺1項以上,可以分別以y1、y2、y3等代表各缺項,然後在計算其中之一時,把其他缺項y直接用符號y1、y2等當作未缺項代人(13)式,這樣可得與缺項數相同的方程組,解方程組即得。
隨機區組設計,當劑量組內安排的區組數較多時,也可將缺項所在的整個區組除去。
隨機設計的實驗結果中,如在個別劑量組多出1~2個反應值,可按嚴格的隨機原則去除,使各劑量組的反應個數m相等。
不論哪種實驗設計,每補足一個缺項,就需把s2的自由度減去1,缺項不得超過反應總個數的5%。
(3)方差分析 方陣表(表二)的實驗結果,按(14)~(21)式計算各項變異的差方和、自由度(f)及誤差項的方差(s2)。
隨機設計 按(14)式、(15)式計算差方和(總)、差方和(劑間)。按(20)式計算差方和(誤差)。按(18)式或(21)式計算s2。
隨機區組設計 按(14)~(17)式計算差方和(總)、差方和(劑間)、差方和(區組間)、差方和(誤差)。按(18)式或(19)式計算s2。

f(總)=mK-1


(4)可靠性測驗 通過對劑間變異的分析,以測驗S和T的對數劑量和反應的關係是否顯著偏離平行直線。(2.2)法和(2.2.2)法的劑間變異分析爲試品間、迴歸、偏離平行三項,其他(k·k)法還需再分析二次曲線、反向二次曲線等。
(k·k)法、(k·k')法按表四計算各變異項的m·∑C2i及∑[Ci·∑y(k)],按(22)式計算各項變異的差方和。
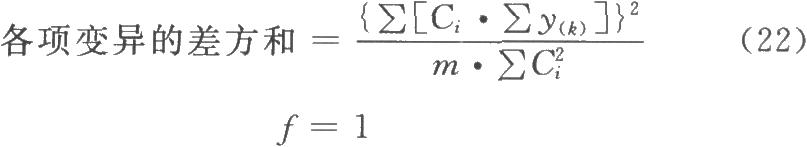
表四 (k·k)法、(k·k')法可靠性測驗正交多項係數表(k·k·k)法按(23)式、(24)式計算試品間差方和。
(2.2.2)法
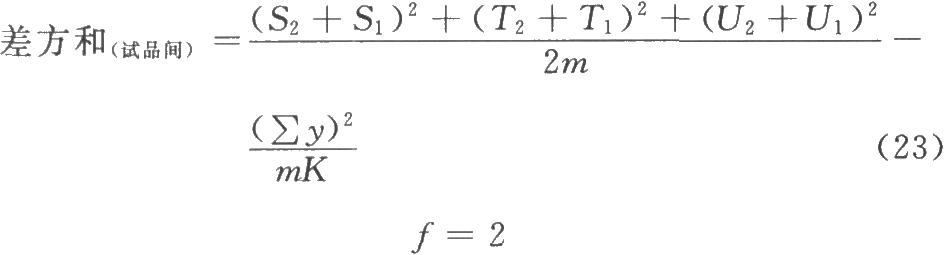
(3.3.3)法
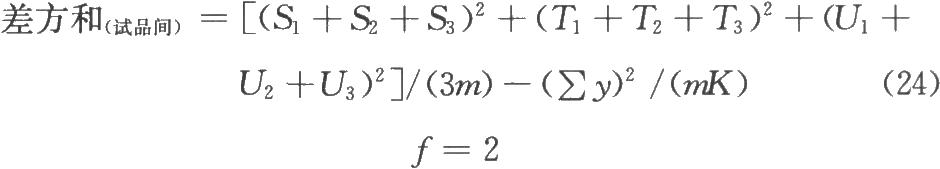
按表五計算迴歸、二次曲線、反向二次曲線各項變異的m·∑C2i及∑[Ci·∑y(k)];按(22)式計算差方和(迴歸)、差方和(二次曲線)。
表五 (k·k·k)法可靠性測驗正交多項係數表
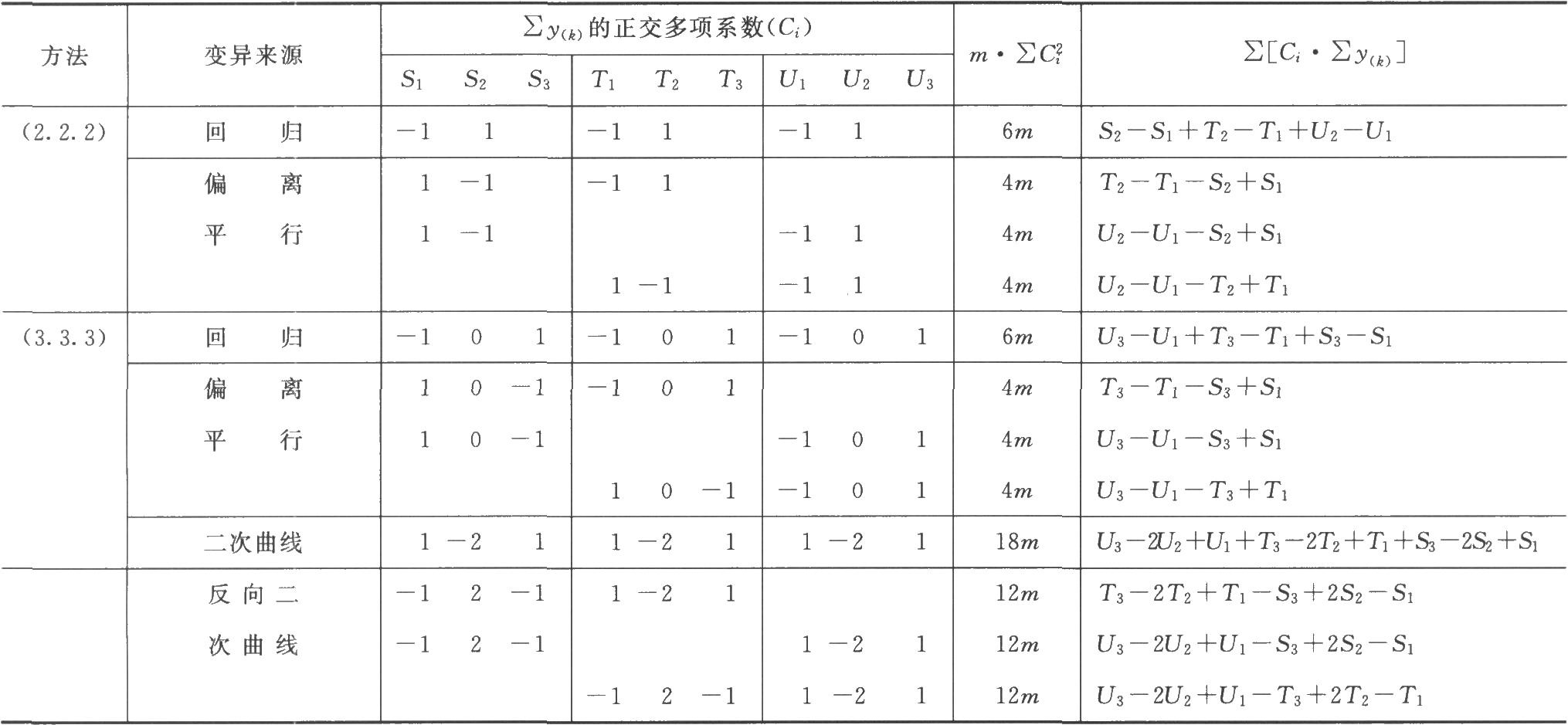
按(25)式計算差方和(偏離平行)及差方和(反向二次曲線)。

將方差分析結果列表進行可靠性測驗。例如隨機區組設計(3.3)法可靠性測驗結果列表,見表六。
裹六 隨機區組設計(3.3)法可靠性測驗結果
變異來源 | f | 差方和 | F | P | |
試品間 迴歸 偏離平行 二次曲線 反向二次曲線 | 1 1 1 1 1 | (22)式 (22)式 (22)式 (22)式 (22)式 | 差方和/f 差方和/f 差方和/f 差方和/f 差方和/f | 方差/S2 方差/S2 方差/S2 方差/S2 方差/S2 | |
劑間 區組間 | K-1 m-1 (K-1)(m-1) | (15)式 (16)式 (17)式 | 差方和/f 差方和/f 差方和/f(s2) | 方差/S2 方差/S2 | |
總 | mK-l | (14)式 |
表六中概率P是以該變異項的自由度爲分子,誤差項(S2)的自由度爲分母,查F值表(表七),將查表所得F值與表六F項下的計算值比較而得。當F計算值大於P=0.05或P=0.01的查表值時,則P<0.05或P<0.01,即爲在此概率水平下該項變異有顯著意義。
可靠性測驗結果,迴歸項應非常顯著(P<0.01)。(2.2)法、(2.2.2)法偏離平行應不顯著(P>0.05)。其他(k·k)法、(k·k·k)法偏離平行、二次曲線、反向二次曲線各項均應不顯著(P>0.05)。
試品間一項不作爲可靠性測驗的判斷標準,試品間變異非常顯著者,重複試驗時,應參考所得結果重新估計T的效價或重新調整劑量試驗。
雙交叉設計的方差分析和可靠性測驗
(1)雙交叉設計實驗結果的方陣表 將動物按體重隨機分成四組,各組的動物數(m)相等,四組的動物總數爲4m。對四組中的每一隻動物都加以識別標記,按雙交叉設計給藥次序表進行實驗,各組的每一隻動物都給藥兩次,共得2×4m個反應值。將S、T各兩個劑量組兩次實驗所得反應值排列成表,見表八。
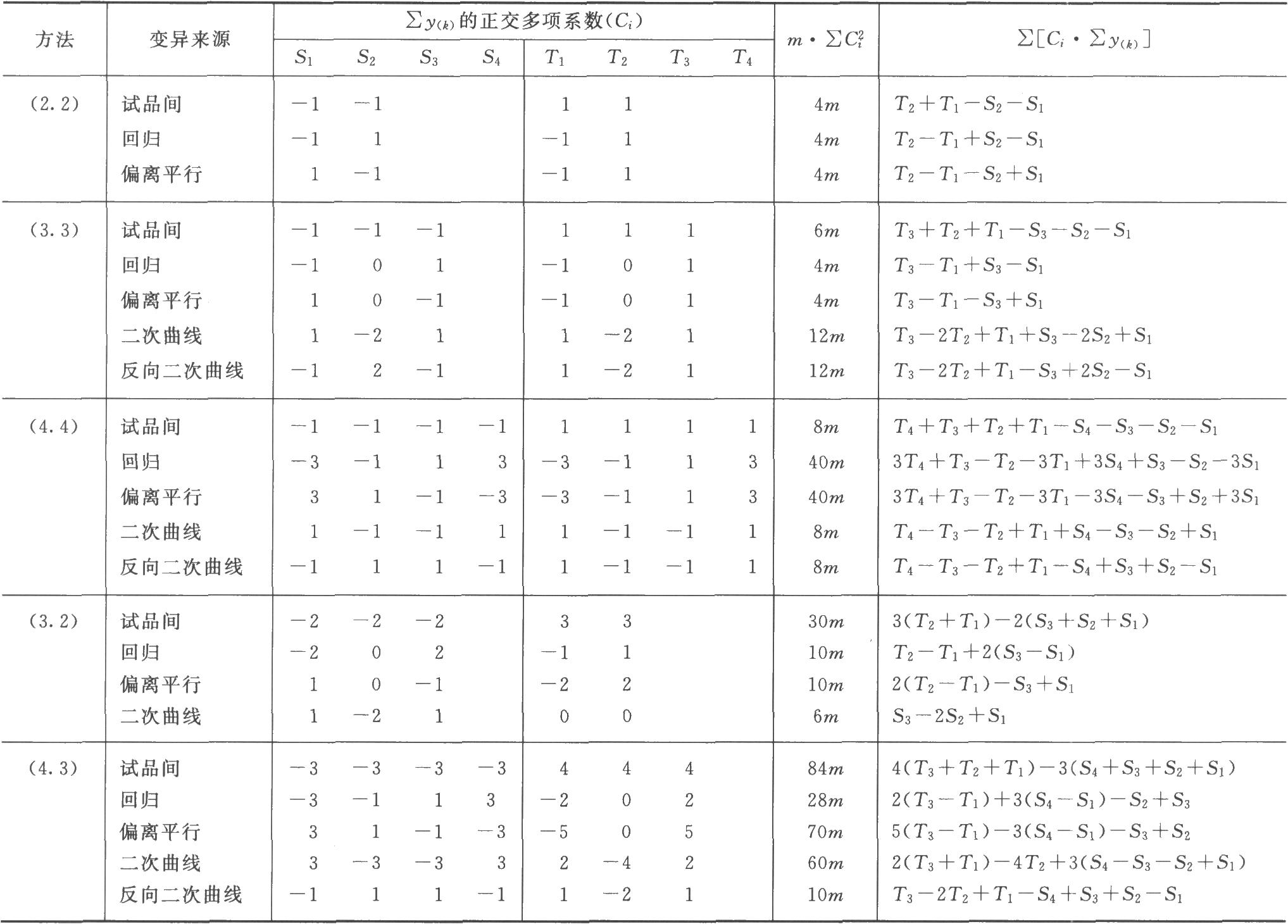
注:用(2.3)法及(3.4)法時,分別將(3.2)法及(4.3)法中S和T的正交多項係數互換即得。
表中S1、S2、T1、T2…在量反應分別爲標準品和供試品每一劑量組內的反應值或它們規定函數的總和[相當於表二的∑y(k)各項]。所有足序1、2、3……都是順次由小劑量到大劑量,Ci是與之相應的正交多項係數。m·∑C2i是該項變異各正交多項係數的平方之和與m的乘積,∑[Ci·∑y(k)]爲S1、S2…T1、T2…分別與該項正交多項係數乘積之和。
表七 F值表
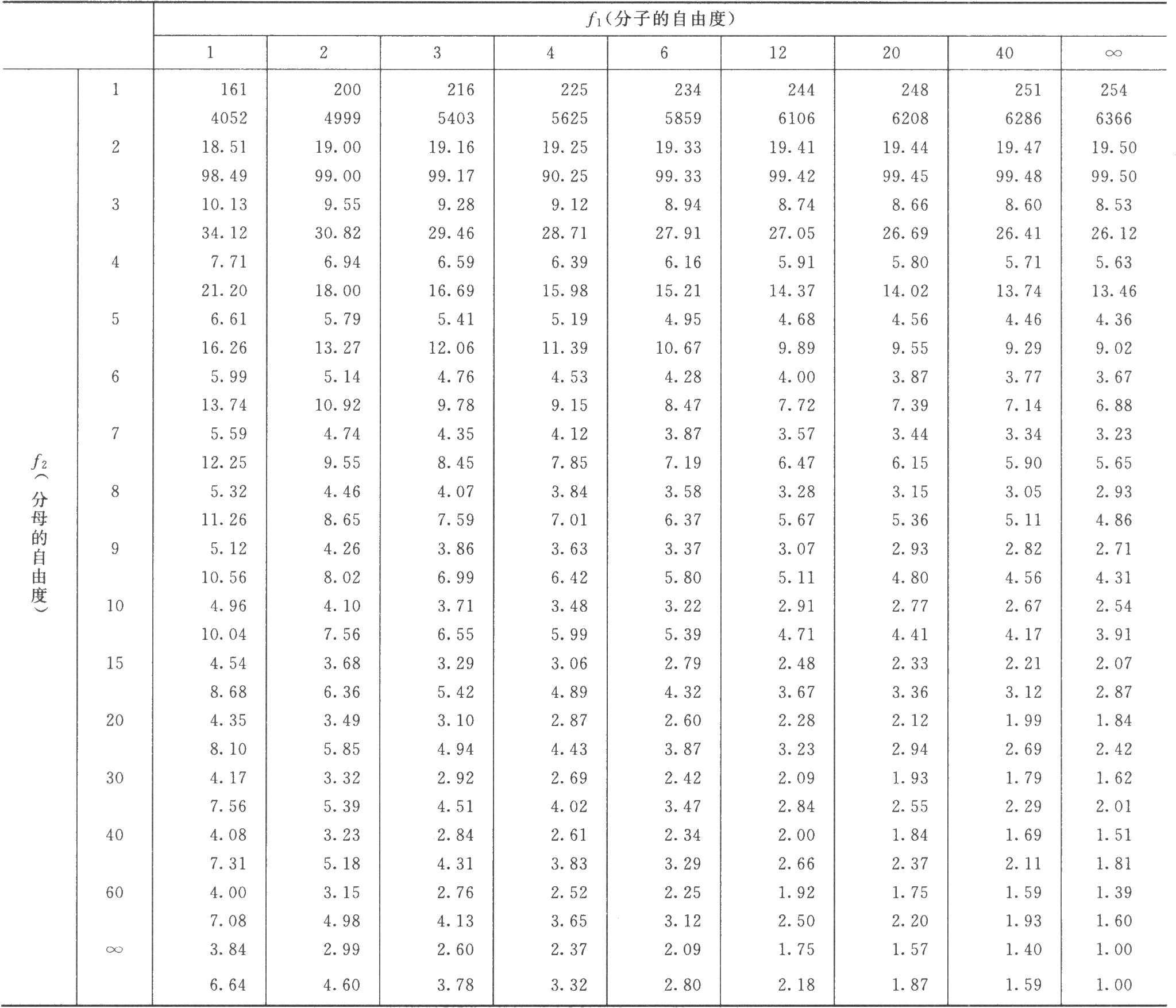
注:上行,P=0.05;下行,P=0.01。
表八 雙交叉實驗結果
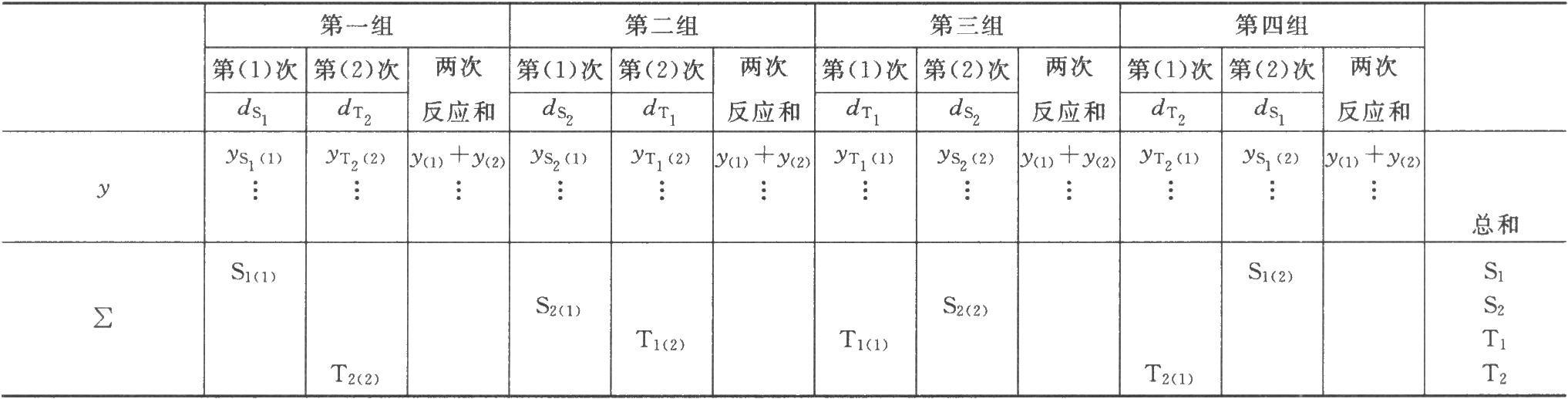
(2)缺項補足 表八中如有個別組的1個反應值因故缺失,均作該只動物缺失處理,在組內形成兩個缺項。此時,可分別用兩次實驗中該組動物其餘各反應值的均值補入;也可在其餘三組內用嚴格隨機的方法各去除1只動物,使各組的動物數相等。每補足一個缺項,誤差(Ⅰ)和誤差(Ⅱ)的方差s2Ⅰ和s2Ⅱ的自由度都要減去1。缺項不得超過反應總個數的
5%。同一組內缺失的動物不得超過1只。
(3)方差分析 雙交叉設計的總變異中,包含有動物間變異和動物內變異。對錶八的2×4m個反應值進行方差分析時,總變異的差方和(總)按(26)式計算。
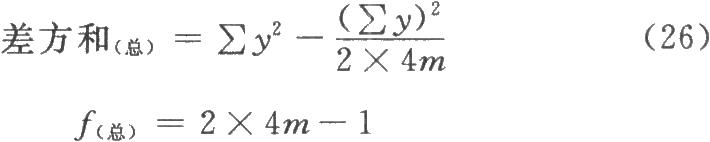
動物間變異是每一隻動物兩次實驗所得反應值的和(表八每組動物的第三列)之間的變異,其差方和按(27)式計算。

動物間變異和動物內變異的分析 將表八中S和T各劑量組第(1)次實驗所得反應值之和S1(1)、S2(1)、T1(1)、T2(1)及第(2)次實驗反應值之和S1(2)、S2(2)、T1(2)、T2(2)按表九雙交叉設計正交係數表計算各項變異的m·∑C2i及∑(Ci·y),按(22)式計算各項變異的差方和。
總變異的差方和減去動物間變異的差方和,再減去動物內各項變異的差方和,餘項爲誤差(Ⅰ)的差方和,按(28)式計算。

誤差(I)的方差s2,用以計算實驗誤差SM、FL,及進行動物內各項變異(表九中*標記者)的F測驗。
誤差(Ⅱ)的差方和爲動物間變異的差方和減去表九中其餘三項變異(表九中無*標記者)的差方和,按(29)式計算。
表九 雙交叉設計正交係數表①

①各項變異的自由度均爲1。有*號標記的四項爲動物內變異,其餘三項爲動物間變異。

(4)可靠性測驗 將方差分析及F測驗的結果列表,如表十。
表十中的概率P,計算同表六,但表的上半部分是以s2Ⅱ的自由度爲分母,表的下半部分以s2的自由度爲分母,查F值表(表七),將查表所得的F值與表十F項下的計算值比較而得。
表十 雙交叉設計可靠性測驗結果

可靠性測驗結果判斷 迴歸、偏離平行、試品間三項的判斷標準同(2.2)法。
次間×試品間、次間×迴歸、次間×偏離平行三項中,如有F測驗非常顯著者,說明該項變異在第一次和第二次實驗的結果有非常顯著的差別,對出現這種情況的檢定結果,下結論時應慎重,最好複試。
4.3 3.效價(PT)及可信限(FL)計算
各種(k·k)法都按表十一計算V、W、D、A、B、g等數值,代入(30)~(33)式及(3)式、(8)式計算R、PT、SM以及R、PT的FL和FL%等。

(2.2)法雙交叉設計 計算方法同上述(2.2)法。雙交叉設計各劑量組都進行兩次試驗,S和T每一劑量組的反應值個數爲組內動物數的兩倍(2m)。
(1)雙交叉設計用S和T各組劑量兩次試驗所得各反應值之和(表八中的S1、S2、T1、T2)按表十一(2.2)法公式計算V、W、D、g等數值。
表十一 量反應平行線檢定法的計算公式①
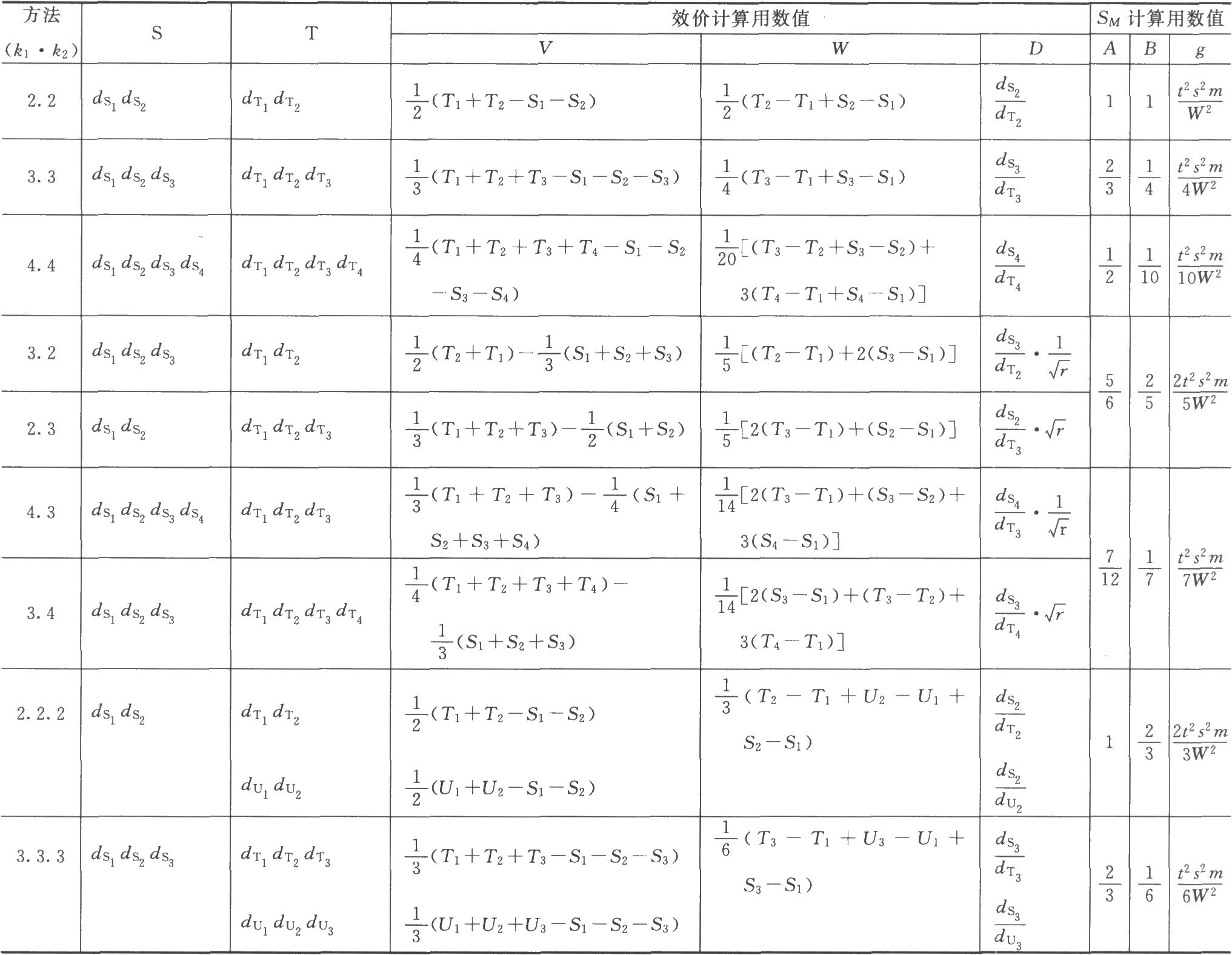
①表中dS、dT分別爲S和T的劑量,下角1、2、3是順次由小劑量到大劑量。
(2)參照(31)式計算SM,因每隻動物進行兩次實驗,式中m用2m代替,(2.2)法A=1,B=1,SM的公式爲
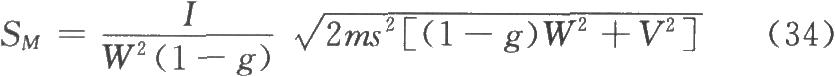

例2 量反應平行線測定隨機設計(3.3.3)法絨促性素(HCG)效價測定——小鼠子宮增重法

表2-1 HCG效價測定結果
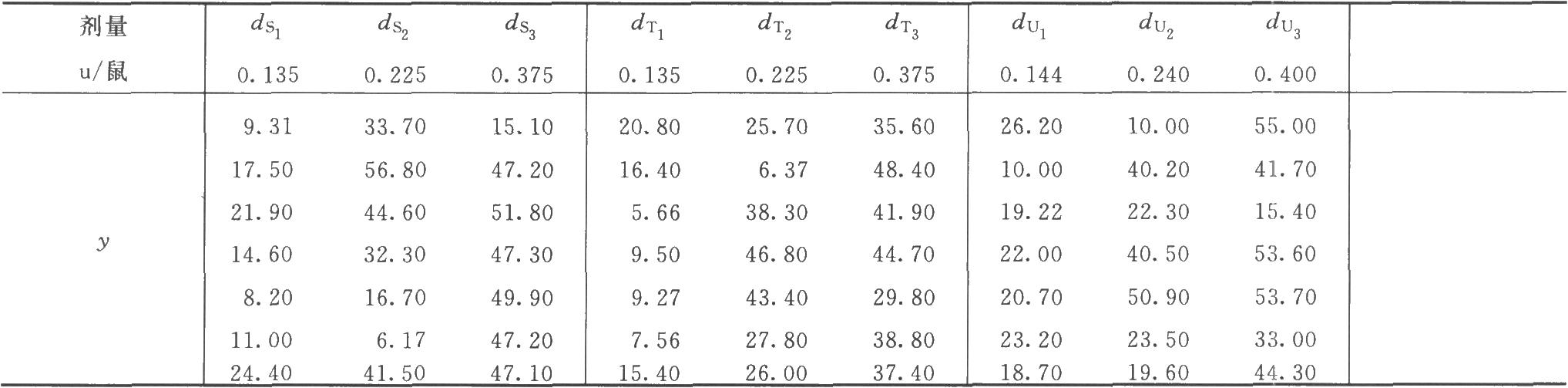
續表
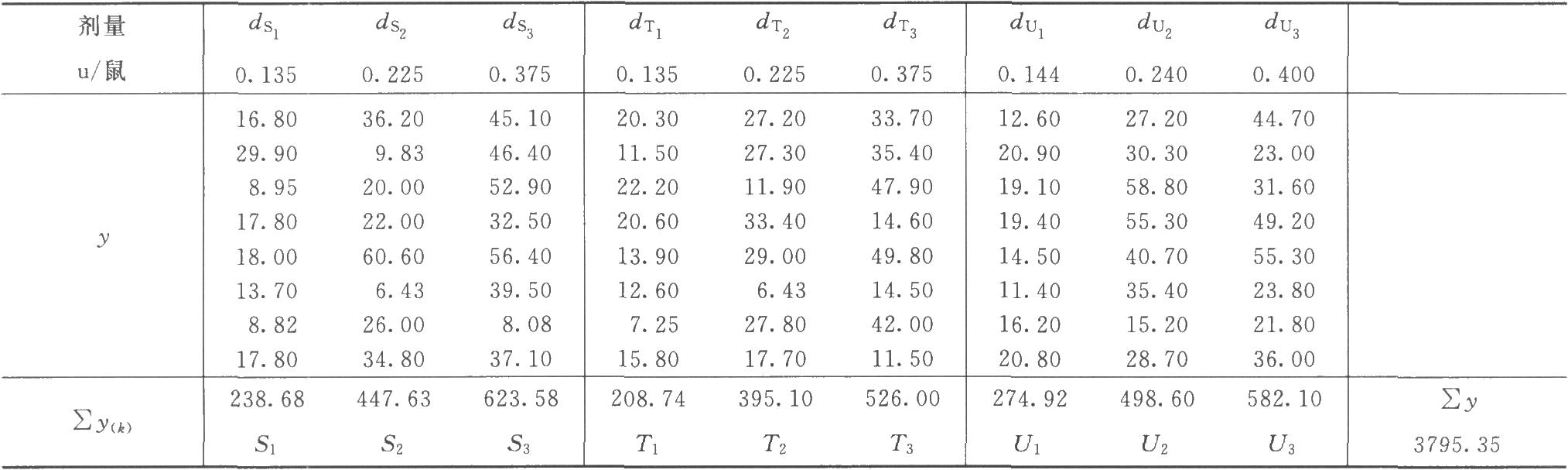
(3.3.3)法,K=9;每組15只小鼠,m=15
(1)按(14)式、(15)式、(20)式計算各項的差方和
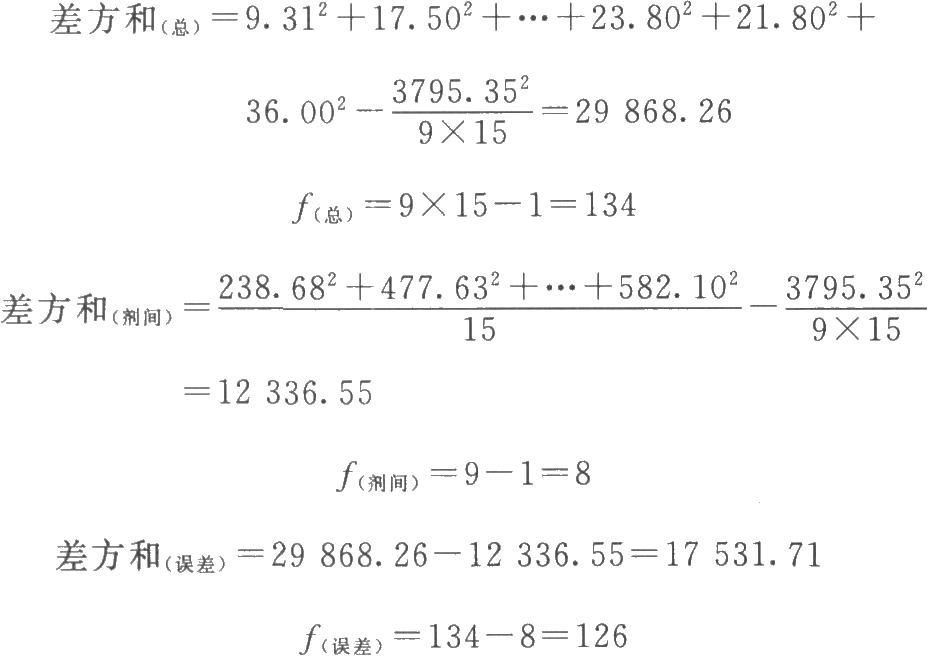
(2)劑間變異分析及可靠性測驗 按(24)式及表五 (3.3.3)法分析。

各項分析結果見表2-2、表2-3。
結論:迴歸非常顯著,偏離平行、二次曲線、反向二次曲線均不顯著,實驗結果成立。

表2-3 HCG效價測定(3.3.3)法可靠性測驗結果

(3)效價(PT、PU)及可信限(FL)計算 按表十一(3.3.3)法及(30)~(33)式、(3)式、(8)式計算。


例3 量反應平行線測定隨機區組設計(3.3)法新黴素效價測定——杯碟法
稀釋液dS1:8.0u/ml ds2:10.:0u/ml ds3:12.5u/ml
T爲新黴素 標示量 AT:670u/mg
稀釋液dT:8.0u/ml
dT2:10.0u/ml
dT3:12.5 u/ml
r=1:0.8
I=0.0969

隨機區組設計(3.3)法,K=6
不同雙碟(碟間)是劑量組內所加的因級限制,共9個雙碟,m=9。
(1)按(14)~(18)式計算各項差方和

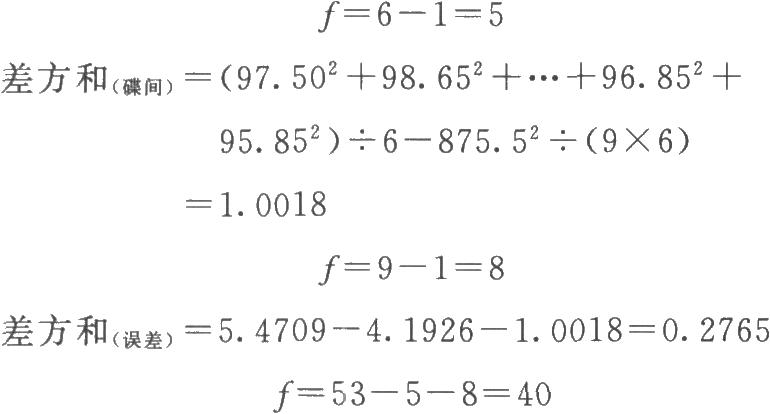
(2)劑間變異分析及可靠性測驗 按表四(3.3)法計算,結果見表3-2、表3-3。
結論:迴歸非常顯著(P<0.01),偏離平行、二次曲線、反向二次曲線均不顯著(P>0.05),實驗結果成立。組內(碟間)差異非常顯著(P<0.01),分離碟間差異,可以減小實驗誤差。
(3)效價(PT)及可信限(FL)計算 按表十一(3.3)法及(30)~(33)式、(3)式、(8)式計算。


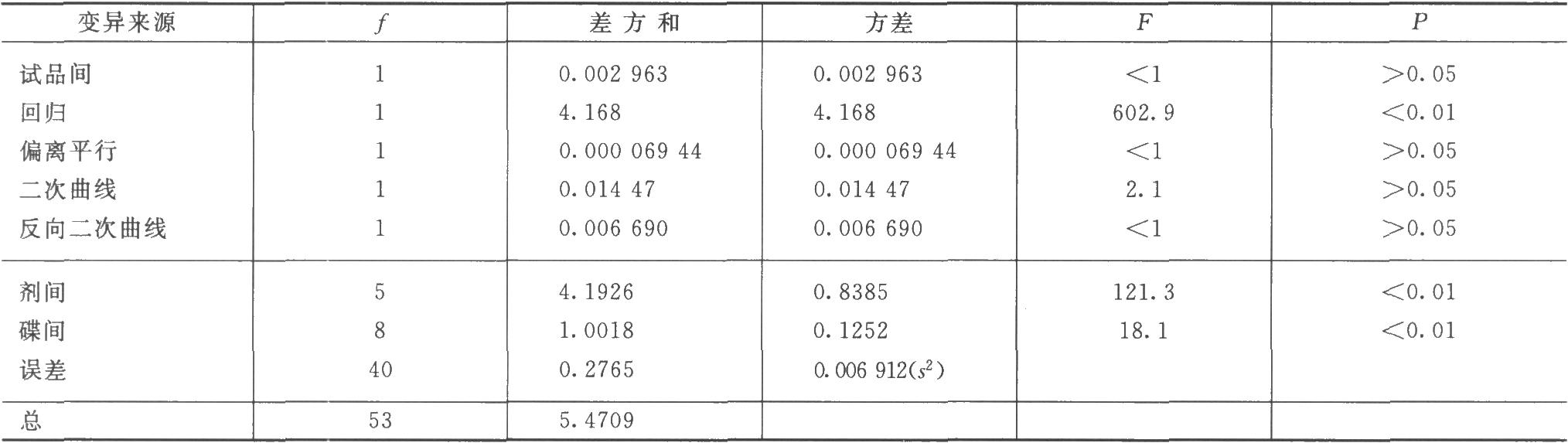


和表3-3結果相同。
例4 量反應平行線測定隨機區組設計(2.2)法縮宮素效價測定——大鼠離體子宮法
dS1:0.0068u dS2:0.009u
T爲縮宮素注射液 標示量AT:10u/ml
dT1:0.008u dT2:0.0106u
r=1:0.75 I=0.125
隨機區組設計(2.2)法,K=4。每組4個劑量爲一區組,其給藥次序爲劑量組內所加因級限制。各劑量組均爲5個反應,m=5。
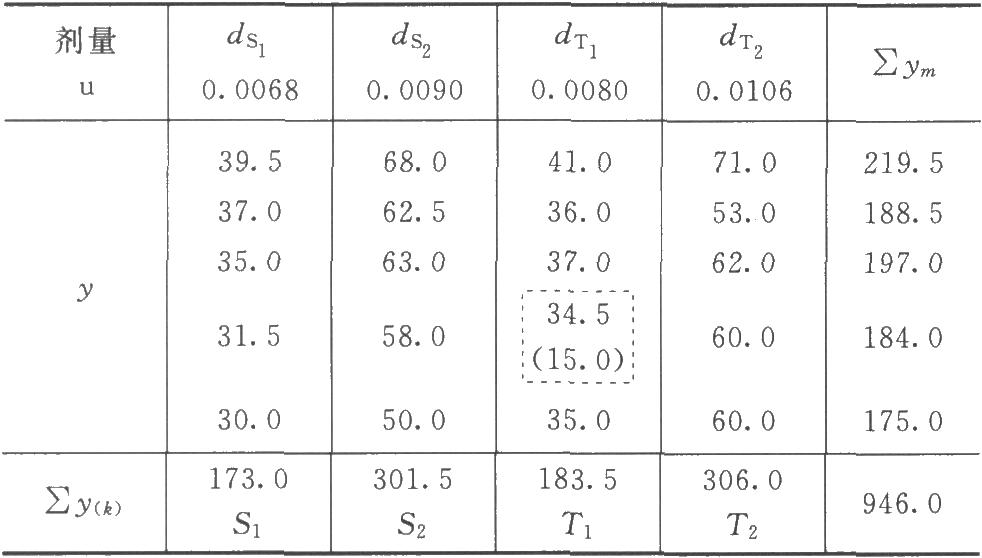
(1)特異反應處理 表4-1第三列第四行dT,的第4個數值特小,本例爲隨機區組設計按(10)式計算決定此值是否屬特異值。
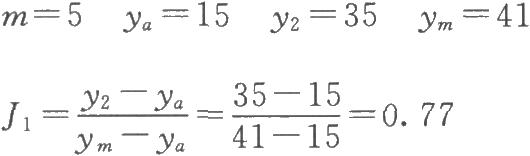
查表三,m=5時,J1=0.73,小於計算值0.77,故此值可以剔除。剔除後形成的缺項按(13)式補足。
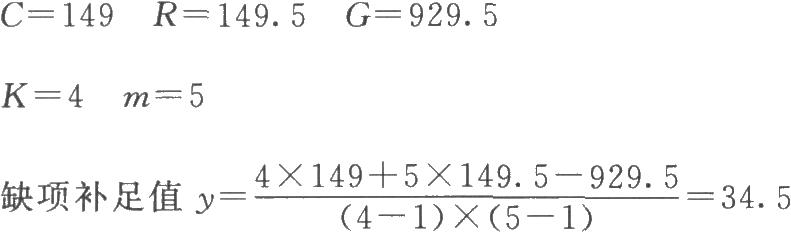
(2)按(14)~(18)式計算各項差方和 補足了一個缺項,誤差項的自由度按(17)式再減1。
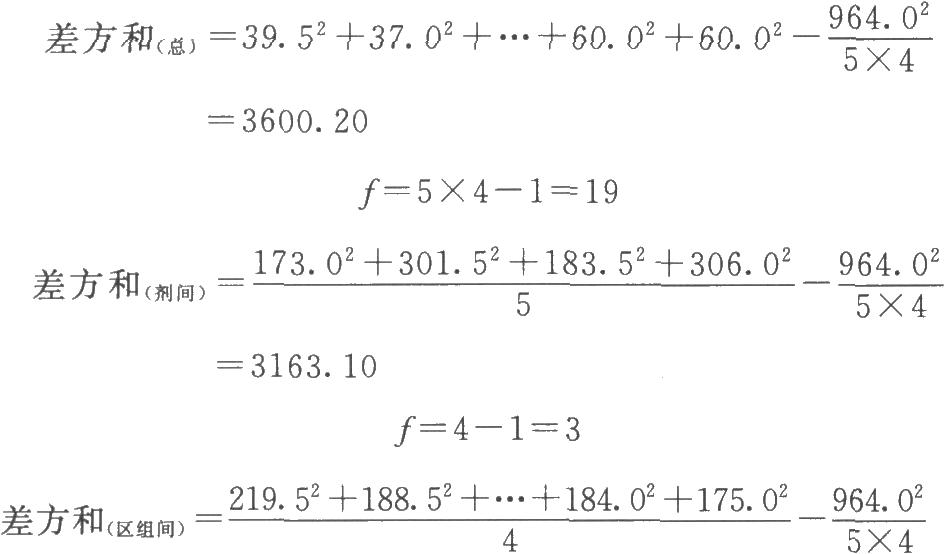
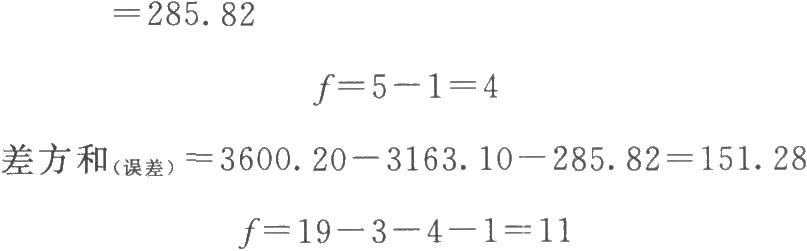
(3)劑間變異分析及可靠性測驗 按表四(2.2)法計算,結果見表4-2、表4-3。
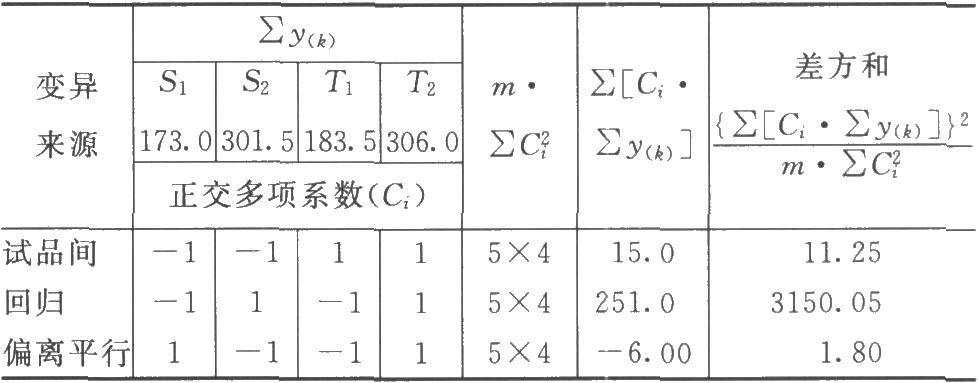
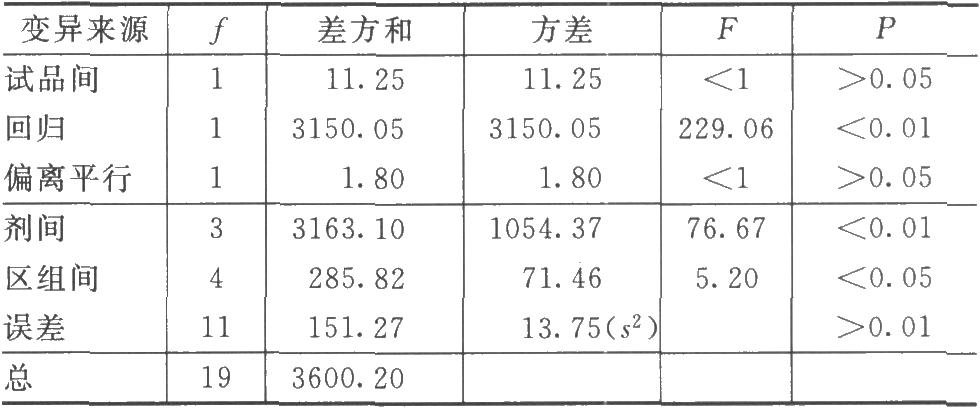
結論:迴歸非常顯著(P<0.01),偏離平行不顯著(P>0.05),實驗結果成立。
區組間差異顯著(P<0.05),分離區組間變異,可以減小實驗誤差。
縮宮素離體子宮效價測定,如區組間變異不顯著,也可以不分離區組間變異,用隨機設計方差分析法計算。
(4)效價(PT)及可信限(FL)計算 按表十一(2.2)法及(30)~(33)式、(3)式、(8)式計算。

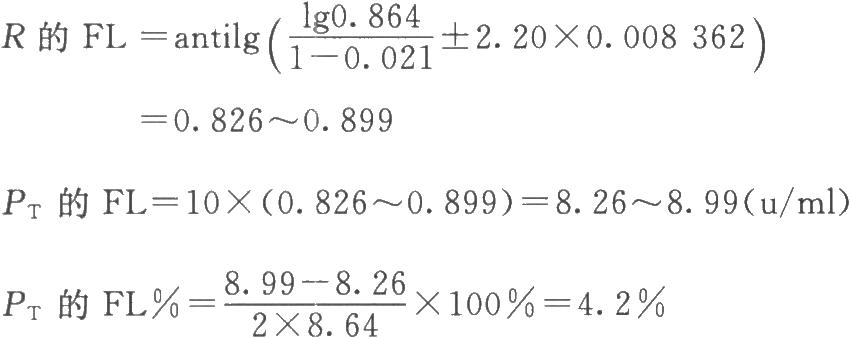
例5 量反應平行線測定(2.2)法雙交叉設計胰島素效價測定——小鼠血糖法

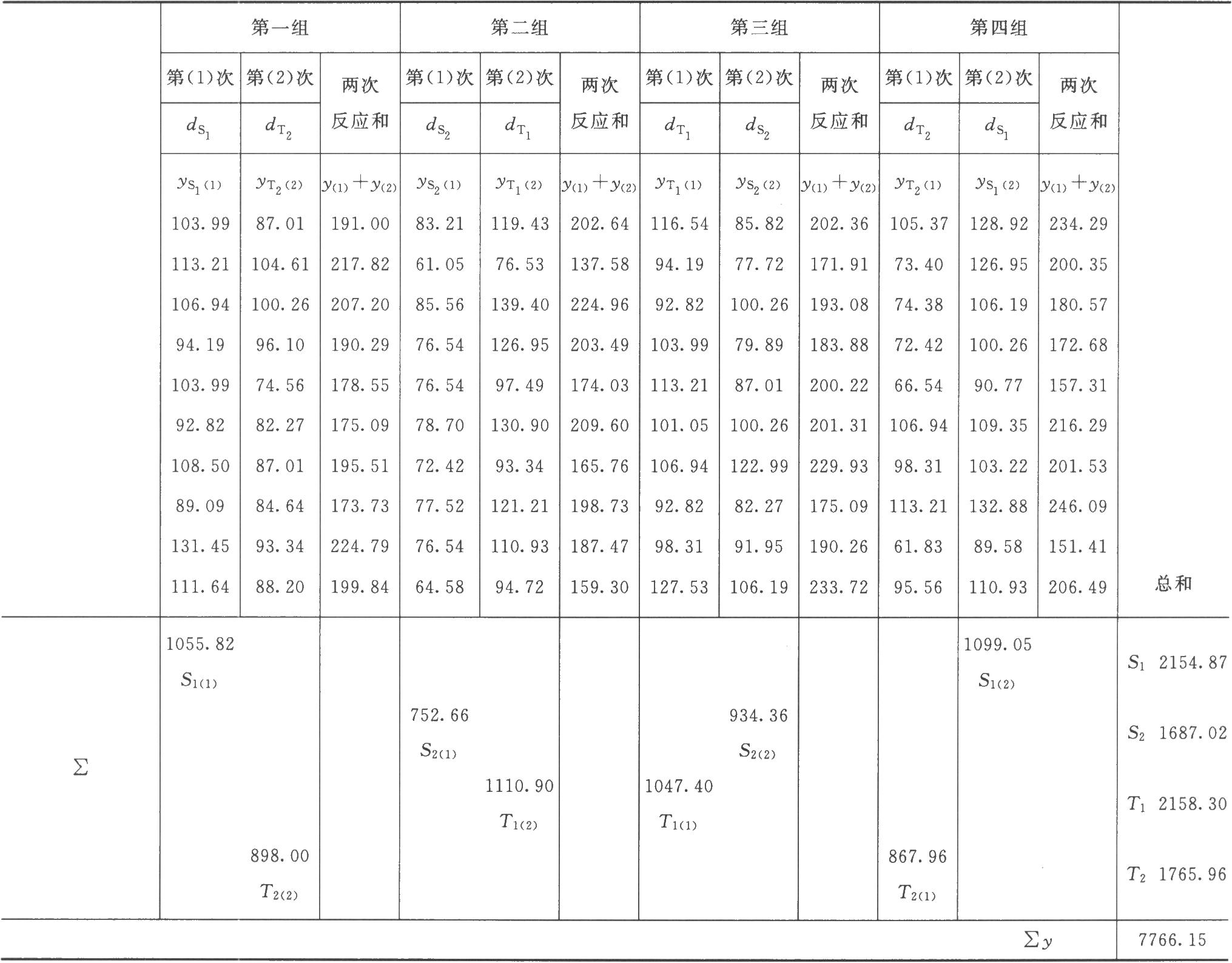
(1)方差分析 按(26)式、(27)式計算:

f(動物間)=4×10-1=39
(2)將表5-1中S、T各劑量組每一次反應值之和按表九及(22)式、(28)式、(29)式、(18)式計算各項變異的m·∑C2i、∑(Ci·∑y)及差方和、方差,並進行可靠性測驗,結果見表5-2、表5-3。按(28)式、(29)式計算:

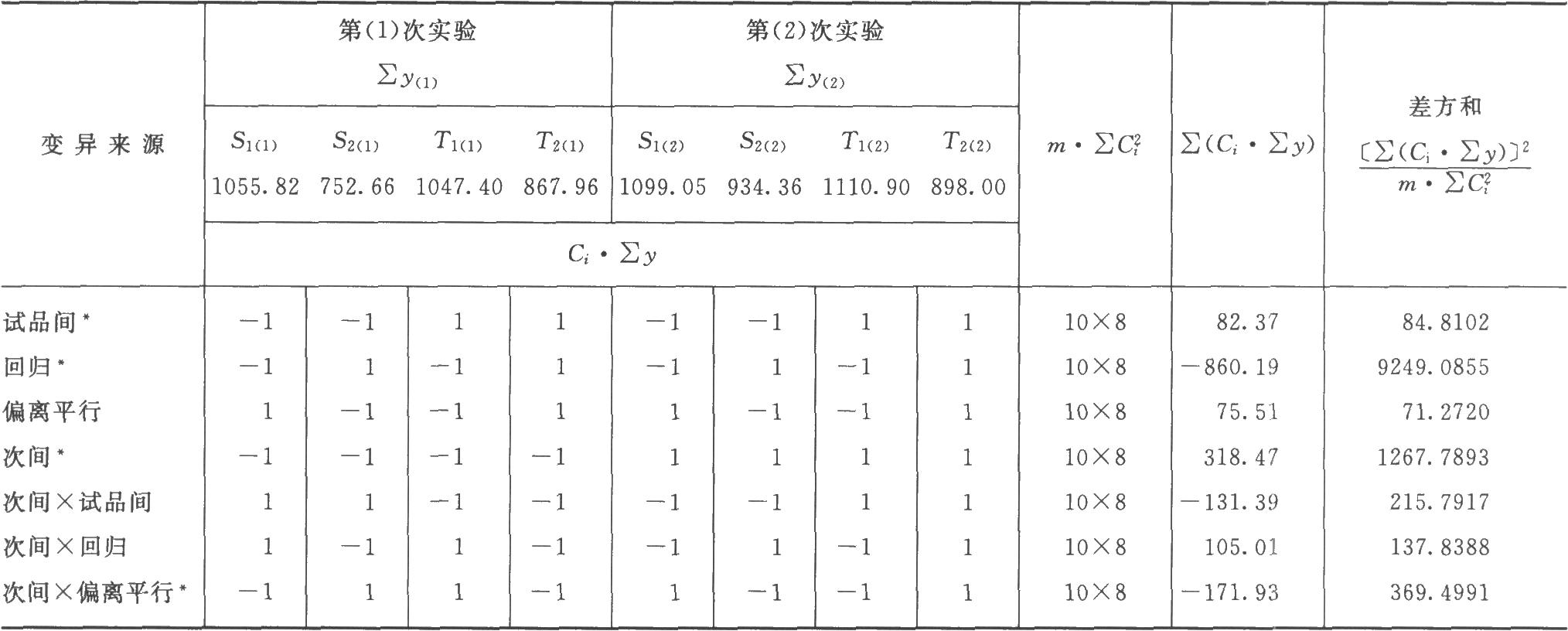
表5-3 胰島素雙交叉法可靠性測驗結果
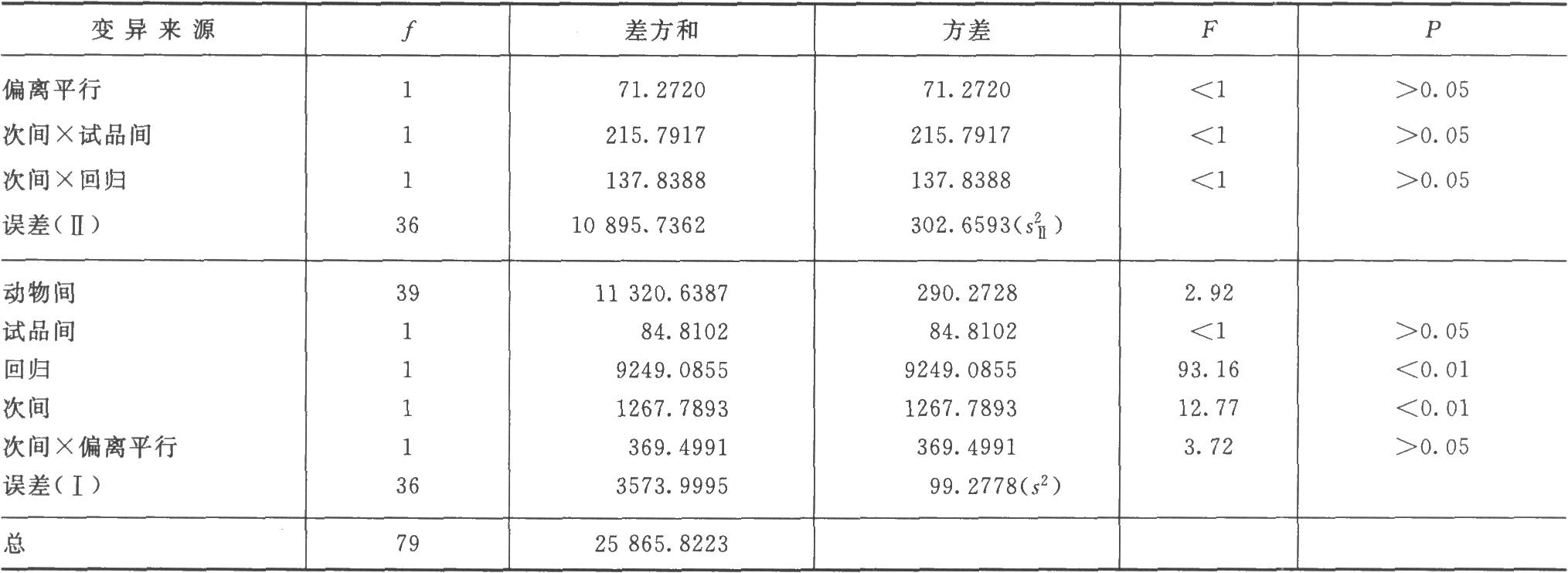

結論:迴歸非常顯著,偏離平行不顯著,實驗結果成立。兩次實驗間的差異非常顯著,用雙交叉設計可以消除實驗間變異對實驗誤差的影響,提高實驗的精確度。
(3)效價(PT)及可信限(FL)計算:
用表5-1的S1、S2、T1、T2,按表十一(2.2)法及(30)式、(32)~(34)式等計算:


四、實驗結果的合併計算
同一批供試品重複n次測定,所得n個測定結果,可用合併計算的方法求其效價PT的均值及其FL。
參加合併計算的n個結果應該是:
(1)各個實驗結果是獨立的,完整的,是在動物來源、實驗條件相同的情況下,與標準品同時比較所得的檢定結果(PT)。
(2)各次檢定結果,經用標示量或估計效價(AT)校正後,取其對數值(lgPT)參加合併計算。
計算時,令lgPT=M
n次實驗結果共n個M值,按(35)式進行X2測驗:
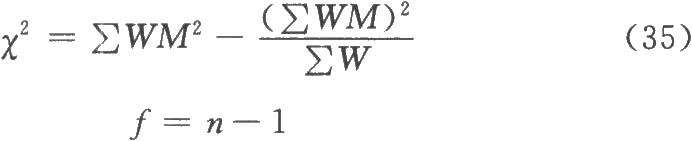
式中W爲各次實驗結果的權重,相當於各次實驗SM平方的倒數,即

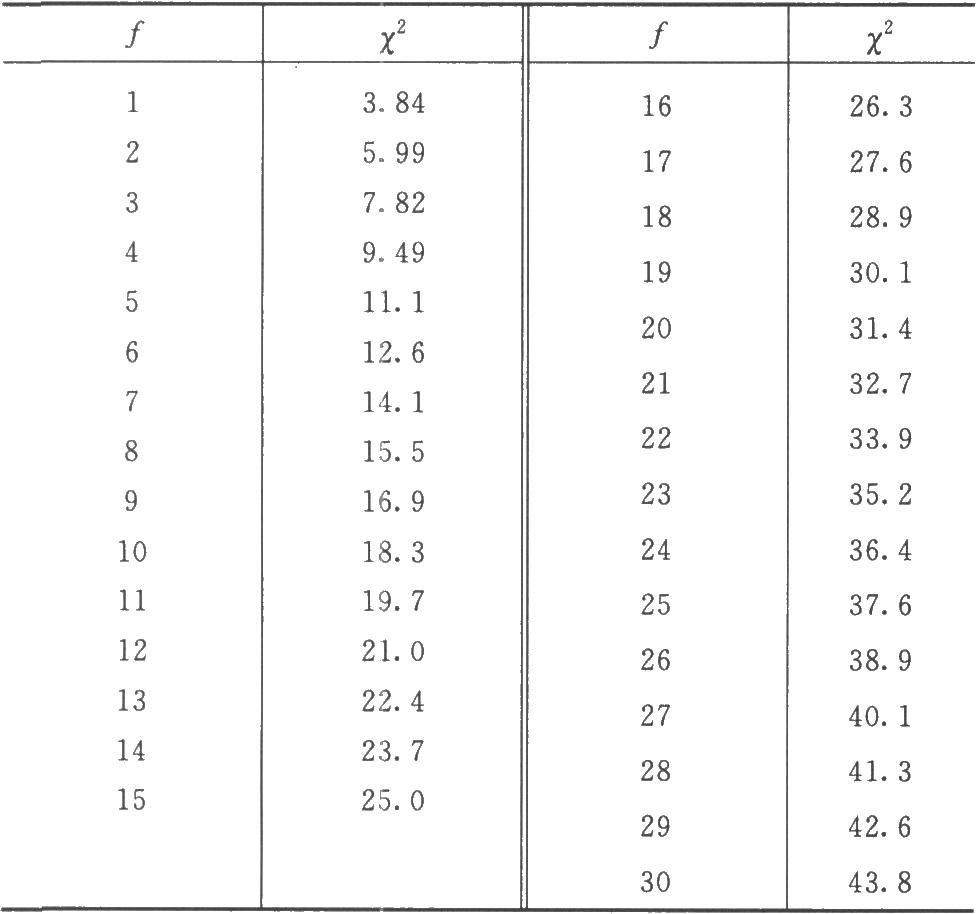
按(35)式的自由度(f)查X2值表(表十二),得X2(f)0.05查表值;當X2計算值小於X2(f)0.05查表值時,認爲n個實驗結果均一,可按(37)式、(38)式、(39)式計算n個M的加權均值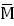 、S
、S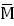 及其FL。
及其FL。
表十二 X2值表(P=0.05)
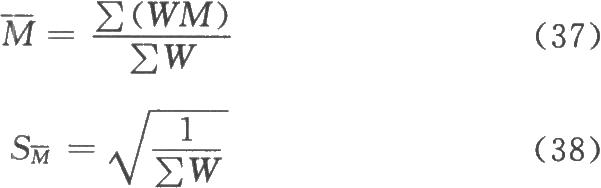
合併計算的自由度(f)是n個實驗結果的s2自由度之和。f=∑fi按此f查t值表(表一)得t值。

PT及其可信限按(40)式、(41)式計算:
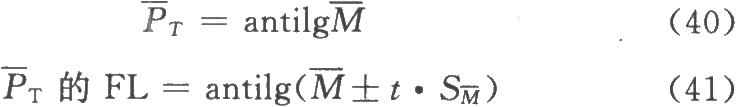
FL%按(8)式計算。
當X2計算值大於X2(f)0.05查表值時,則n個實驗結果不均一,可用以下方法進行合併計算。
(1)如爲個別實驗結果影響n次實驗結果的均一性,可以剔除個別結果,將其餘均一的結果按以上公式進行合併計算,但剔除個別結果應符合“特異反應剔除”的要求。
(2)如果n次實驗結果的不均一性並非個別實驗結果的影響,則按(42)式、(43)式計算校正權重W',如經公式(43)計算結果爲負值,可以刪除減號後面一項,計算近似的S2m和各次實驗的W’。用W'和∑W'代替公式(37)、(38)中W和∑W計算M、SM,再按(39)式、(40)式、(41)式計算M的FL、PT及其FL。

例6 肝素鈉5次測定結果的合併計算測定結果見表6-1。
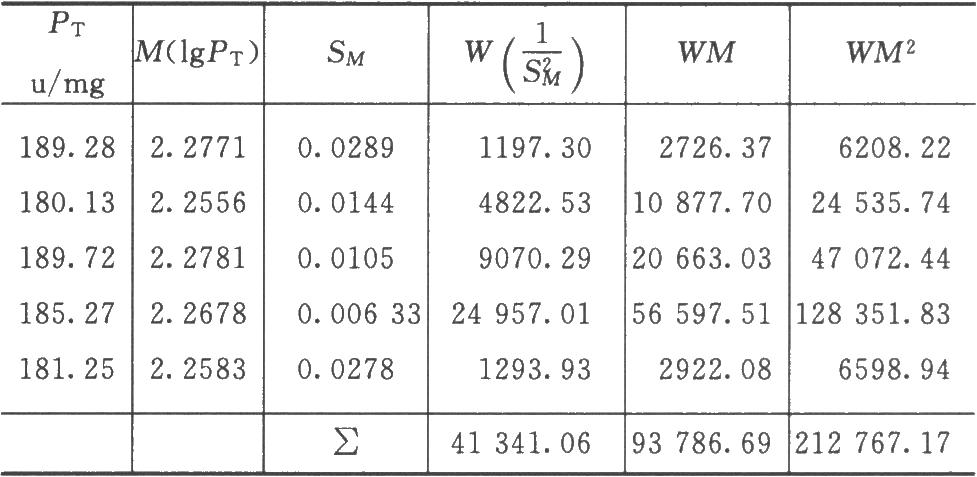
按(35)式計算:
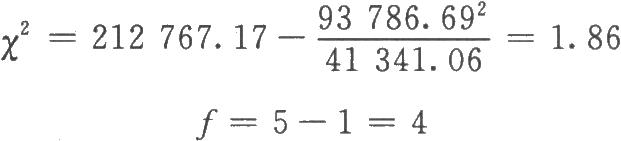
查表十二,X2(4)0.05=9.49
X2計算值1.86
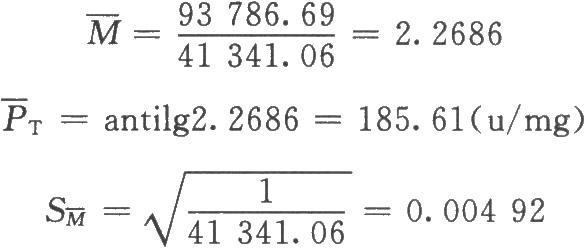
5次實驗均用(3.3)法,隨機設計,每劑5管,各次實驗s2的自由度fi均爲:fi=29-5=24。
合併計算的自由度f=5×24=120,t=1.96

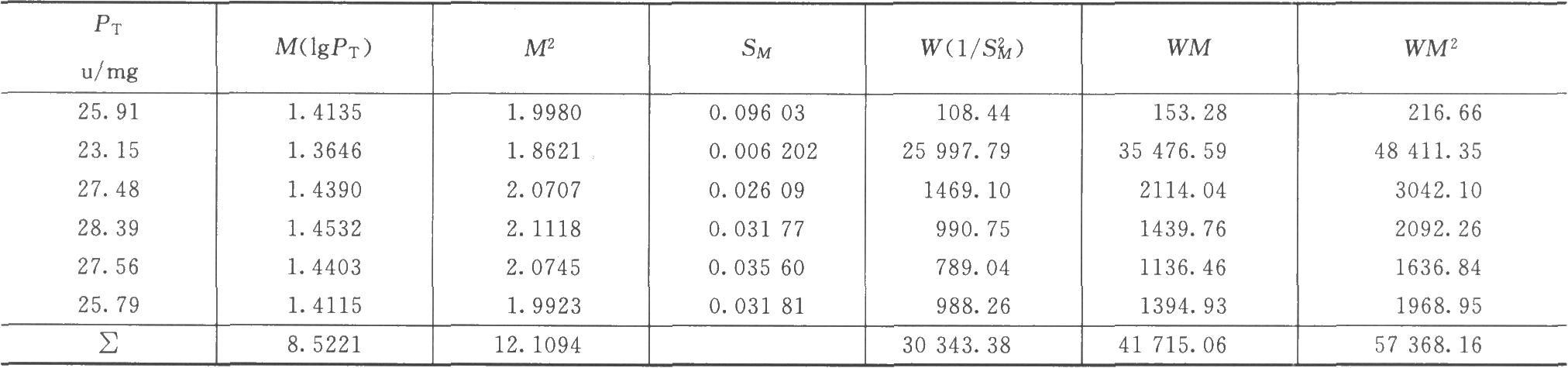
按(35)式:

X2計算值19.70> X2(5)0.05查表值,6次結果不均一,經特異反應剔除計算(公式10),無個別刪除結果。
按(42)式、(43)式計算:

計算結果爲負數,可刪除減號後面項,S2m=0.001007。
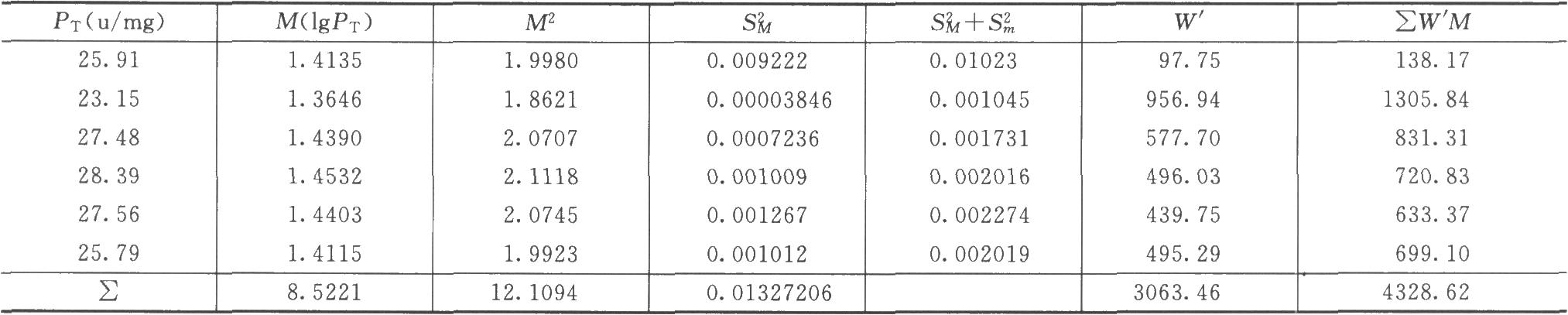
計算各次實驗結果的差方S2M、差方和(S2M+S2m)、校正權重W'、∑W'M,見表7-2。
表7-2 胰島素測定結果不均一時計算表
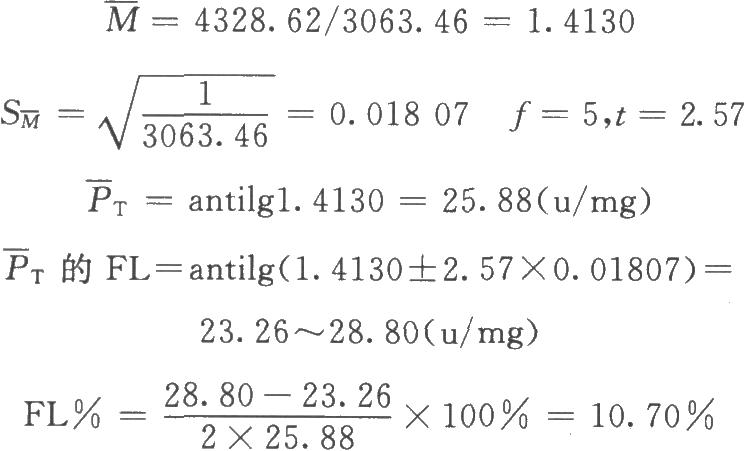
5 五、符號
A SM計算公式中的數值
C 缺項所在列各反應值之和
dS1,dS2…標準品的各劑量dT1,dT2…供試品的各劑量F兩方差值之比,用於方差分析等
FL 可信限
FL% 可信限率
f 自由度
G 缺項補足式中除缺項外各反應值之和
g 迴歸的顯著性係數
I 相鄰高低劑量比值的對數,I=lgr
J1,J2…特異反應剔除用的J值
K S和T的劑量組數和
k·k' S或T的劑量組數
M S和T的對數等反應劑量之差,即效價比值(R)的對數,M=lgR。合併計算中M=lgPT
n S和T反應個數之和
nS 最小效量法S反應的個數
nT 最小效量法T反應的個數
P 概率
PT、PU 供試品(T、U)的測得效價
R 缺項所在行反應值之和
S1,S2… 平行線測定標準品(S)各劑量組反應值之和,等於S各劑量組的∑y(k)
SM M的標準誤
S2 實驗的誤差項
S2m 合併計算中各次實驗間的差方
T 供試品
T1,T2… 平行線測定供試品(T)各劑量組反應值之和,相當於T各劑量組的∑y(k)
t 可信限計算用t值,見表一
U 供試品的另一符號
U1,U2… 平行線測定供試品(U)各劑量組反應值之和,相當於U各劑量組的∑y(k)
u 供試品的效價單位
W 合併計算中爲各次實驗結果的權重
W' 合併計算中各次實驗結果的校正權重
WC 權重係數
nWC 權重
x 對數劑量,x=lgd
XS S的對數劑量或S的對數最小效量
XT T的對數劑量或T的對數最小效量
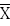 S 直線測定法中,S組對數最小效量的均值
S 直線測定法中,S組對數最小效量的均值
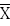 T 直接測定法中,T組對數最小效量的均值
T 直接測定法中,T組對數最小效量的均值
ya、ym 特異反應所在組的兩極端值
∑ 總和
X2 卡方
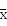 T
T