3 註解
卡方測驗是測定實測值與理論值間符合程度的一種統計方法。如發現實測值與理論值有差異時,就需確定該差異是由於隨機抽樣誤差還是由於理論假說有問題而引起的。通常首先建立無效假說,即認爲觀測值與理論值的差異是由於隨機誤差所致;再確定由於隨機誤差而導致該特定差異的概率;最後根據該概率作出相應的結論,如該概率大於某特定概率標準(即顯著水準,生物統計學上一般定爲0.05),則認爲無效假設成立,即實測值與理論值的差異是由於隨機誤差引起的,進而得出實驗值與理論值相符合的結論。以下結合例子說明x2測驗的分析過程。大麥的六棱有芒品種與二棱無芒品種雜交,F2代的結果爲:二棱有芒132株,六棱有芒38株,二棱無芒42株,六棱無芒14株,試問這兩個性狀是否獨立遺傳,即該四種表型數之比是否符合9∶3∶3∶1的理論比?(1)建立無效假設,假定實驗值與理論值的差異是由於隨機誤差造成的,即實驗數據均取自上述四種表型的比數爲9∶3∶3∶1的總體。(2)計算差異度量值x2值,以便對無效假設進行檢驗,其公式爲
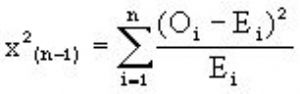
其中x2爲差異度量值,Oi爲第i類觀察數值,Ei爲第i類理論值,n爲類型數,n-1爲自由度(df)。本例觀察總數爲226株,E1=226×9/16=127.125株,E2=E3=226×3/16=42.375株,E4=226×1/16=14.125株,得下表:
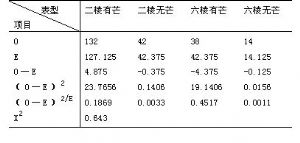
(3)從無效假設出發,根據實得的x2值與自由度查x2表,可確定因隨機誤差造成該差異度量值(x2=0.643)的概率P,x2表見下(這裏僅列出10個自由度):
不同x2值和不同自由度時的P值
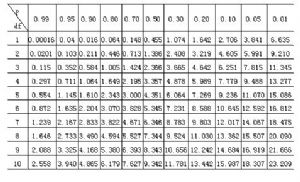
表中第一列爲自由度(df),第一行爲P值,表中所列的數值爲不同的df和P所對應的x2臨界值。當df=4-1=3,實測x2=0.643時,查得 0.80<P<0.90。(4)判斷,查表所得的P值可作爲接受或拒絕無效假說的依據,若由於隨機誤差所造成的差異度量值x2值的概率P≤0.05或實得x2值≥x2(0.05)臨界值時,則認爲實驗值與理論值間的差異顯著,拒絕無效假設,進而得出實驗值與理論值不符合的結論。相反,如果P>0.05或實得x2值<x2(0.05)臨界值,則認爲該差異不顯著,接受無效假設,可得出實驗值與理論值相符合的結論。本例0.80<P<0.90,即P>0.05,或實得x2=0.643<x2(0.05)=7.815臨界值,所以實驗觀察值與理論值間的差異不顯著,接受無效假設,即上述四種表現型數比符合9∶3∶3∶1,因而屬獨立遺傳。